在物理思維過程中，借助相似理論，論證模型與原型的相似性以及將模型實(shí)驗(yàn)的結(jié)果外推到原型中去的合理性的一種認(rèn)識方法。

據(jù)黃金南等所著《科學(xué)發(fā)現(xiàn)與科學(xué)方法》一書介紹，自伽利略提出相似現(xiàn)象的“尺寸效應(yīng)”問題之后，人們深感物理實(shí)驗(yàn)中的模擬方法使用都是以模型與原型之間的物理相似為基礎(chǔ)的。模型與原型具有相同的物理本質(zhì)，各有關(guān)同名物理量相似，各相應(yīng)量之間存在著相同的關(guān)系。1686年牛頓在《自然哲學(xué)之?dāng)?shù)學(xué)原理》一書中，根據(jù)力學(xué)系統(tǒng)中力、質(zhì)量、長度與時間之間的關(guān)系，首先提出了機(jī)械力學(xué)系統(tǒng)的相似法則，被稱之為牛頓的相似判據(jù)：

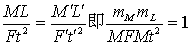
法國的別爾特朗在牛頓基礎(chǔ)上，于1848年利用相似變換的方法，證明了上述機(jī)械運(yùn)動相似的普遍性質(zhì)，構(gòu)成了相似第一定理：相似系統(tǒng)應(yīng)有相同的相似判據(jù)，其相似指數(shù)應(yīng)等于1。隨有模擬方法的進(jìn)一步應(yīng)用，提出了如何找出描述一個物理系統(tǒng)相似判據(jù)的個數(shù)，并確定這些判據(jù)的表達(dá)式的要求，1911年到1914年先后由俄國的A·費(fèi)爾吉曼和美國的E·波根開提出了第二相似定理 (又叫π定理)。指出聯(lián)系n個表征度研究現(xiàn)象的物理量的關(guān)系方程式，可以用這些物理量的 (n—R) 個 [注：R為量綱不同的物理量的個數(shù)]元量綱比數(shù)π(即相似判據(jù)) 完全表達(dá)出來：

f(π₁，π₂，…，π_n-k)=0

但是，第一、二相似定理規(guī)定了相似現(xiàn)象所具有的性質(zhì)，并不是說滿足這兩條定理的現(xiàn)象就一定相似。于是，1930年蘇聯(lián)的基爾皮契夫創(chuàng)立了相似第三定理，進(jìn)一步規(guī)定了相似的必要充分條件，指出：如果現(xiàn)象的單值條件 (系統(tǒng)的幾何性質(zhì)，介質(zhì)的物理性質(zhì)，起始條件和邊界條件等) 相似，并且由這些單值條件所組成的判據(jù)在數(shù)值上相等，則這些現(xiàn)象是相似的。

這三條相似定理為我們定量地設(shè)計(jì)和建立了研究對象相似的模型，以及將對模型實(shí)驗(yàn)結(jié)果正確地定量地外推到原型客體中去提供了一個準(zhǔn)則，它是物理模擬方法的理論思維方法。